リレーショナルデータベースデザイン

　情報無損失分解とは、あるリレーションにおいてその分解成分の自然結合をとると復元できるもののことをいいます。

　リレーションR（A1,A2,...,An）が２つの射影R[X1]とR[X2] （X1∩X2≠φ（空集合）かつX1∪X2＝｛A1,A2,...,An｝）に分解されたとする。
X1∩X2＝｛A1,A2,...,Al｝
X1−（X1∩X2）＝｛B1,B2,...,Bn｝
X2−（X1∩X2）＝｛C1,C2,...,Cm｝
とおく、ようするにリレーションR(A1,A2,...,Al，B1,B2,...,Bn，C1,C2,...,Cm)が２つの射影 R[A1,A2,...,Al，B1,B2,...,Bn]（これをR1とする）とR[B1,B2,...,Bn，C1,C2,...,Cm]（これをR2とする） に情報無損失分解されるための条件について考える。要するにどのようなときにR=R1*R2が成立するかを考える。

R ⊆ R1 * R2　が常に成立する。

　これは、リレーションを適当に分解してしまうと自然結合をとってももとのリレーションが一般には復元できないことと関係している。 要するにA1,A2,...,Al，B1,B2,...,Bn，C1,C2,...,Cmを適当に選んで選んだ分解はリレーションの損失分解になる。

　例えば図１のリレーションにおいて、一方を属性集合｛顧客名，商品名｝、他方を｛商品名，数量，単価，金額｝上の 射影として分解するとき、それは情報損失分解でそれらの自然結合の結果、図４のように元のリレーションには 戻らず、さらに怪しげなタプルが出現し実世界において危険性のある結果リレーションが現れる。このような現象を 結合の罠（connection trip）という。

　そこで、以下の定理を考える必要がある。

リレーションR(A1,A2,...,Al，B1,B2,...,Bm，C1,C2,...,Cn）が２つの射影R[A1,A2,...,Al，B1,B2,...,Bm] とRR[A1,A2,...,Al，C1,C2,...,Cn]に情報無損失分解されるための必要かつ十分条件は、 t[A1,A2,...,Al]＝t'[A1,A2,...,Al]を満たすRの任意の２タプルtとt'について、 それから構成される次の２タプルwとw'がまたRの元であること：
w ＝（t[A1,A2,...,Al，B1,B2,...,Bm]，t'[C1,C2,...,Cn]）
w' ＝（t'[A1,A2,...,Al，B1,B2,...,Bm]，t[C1,C2,...,Cn]）

図１．リレーション注文

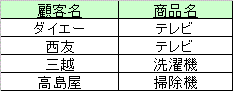
図２．｛顧客名，商品名｝上の射影

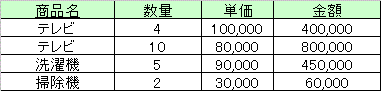
図３．｛商品名，数量，単価，金額｝上の射影

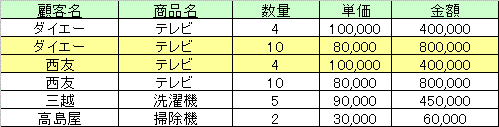
図４．情報損失分解（肌色の部分は元のリレーションにはなかった情報）

戻る